반응형
학습 내용
- 자료구조 중 트리(Tree) 구조의 개념 이해
- 이진 트리와 이진 탐색트리
- Python 링크드 리스트 생성에 이진 탐색 트리 적용하기
🌲 대표적인 자료 구조 트리(Tree)
트리구조는 성능도 좋고, 많이 사용하는 자료구조입니다.
node라는 개념으로 1차원적인 리스트 라는 배열의 개념을 확장한 느낌이 드는 데요.
node와 branch를 이용해서, 마치 나무가 뿌리를 내린듯한 구조로 탐색 알고리즘 구현을 위해 많이 사용됩니다.
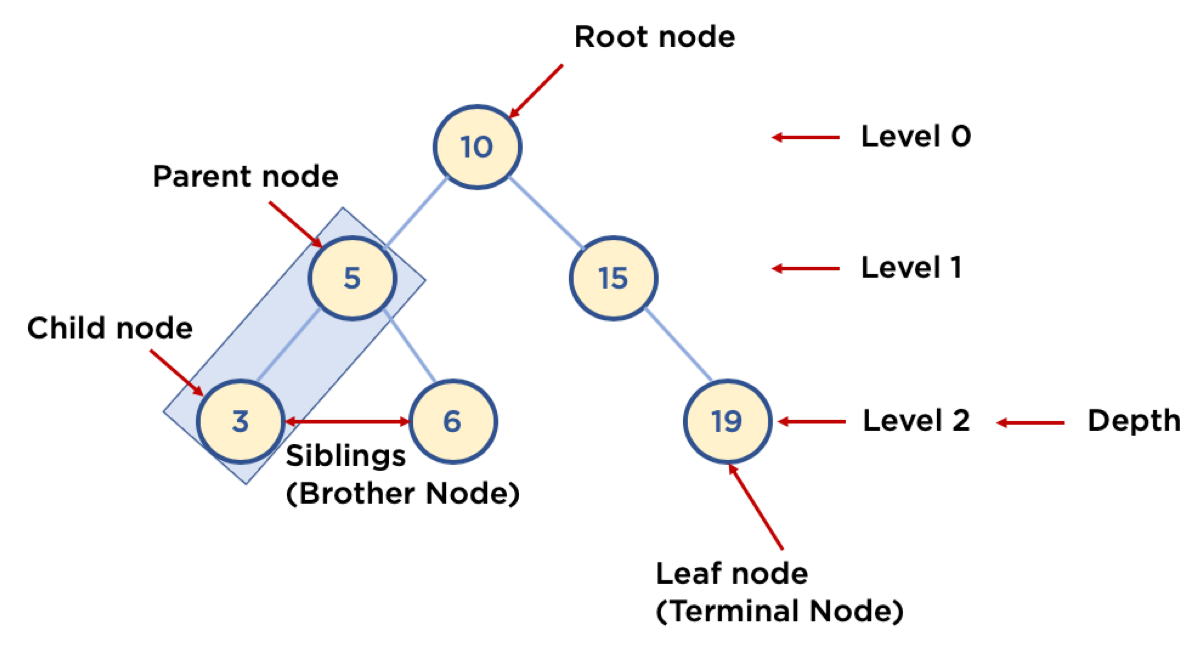
트리(Tree) 관련 용어 정리
- Node: 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
- Root Node: 트리 맨 위에 있는 노드
- Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 다음 레벨에 연결된 노드
- Child Node: 어떤 노드의 상위 레벨에 연결된 노드
- Leaf Node (Terminal Node): Child Node가 하나도 없는 노드
- Sibling (Brother Node): 동일한 Parent Node를 가진 노드
- Depth: 트리에서 Node가 가질 수 있는 최대 Level
🌿 이진 트리와 이진 탐색 트리 (Binary Search Tree)
이진트리와 이진 탐색트리는 이름은 비슷하지만 다른 개념입니다.
이진 탐색트리에는 '조건'이 붙기 때문인데요.
이 조건을 활용하면 탐색 알고리즘을 구현 할 때, 매우 빠른 성능을 낼 수 있습니다.
- 이진 트리: 노드의 최대 Branch가 2인 트리(Tree)
- 이진 탐색 트리 (Binary Search Tree, BST): 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음!
- 이러한 조건으로 인해 더 빠른 데이터 탐색이 가능함. (vs 일반 배열구조)

이진 탐색트리의 장점과 주요 용도
- 주요 용도: 데이터 검색(탐색)
- 장점: 탐색 속도를 개선할 수 있음, 데이터 삽입 시에도 속도가 빠름
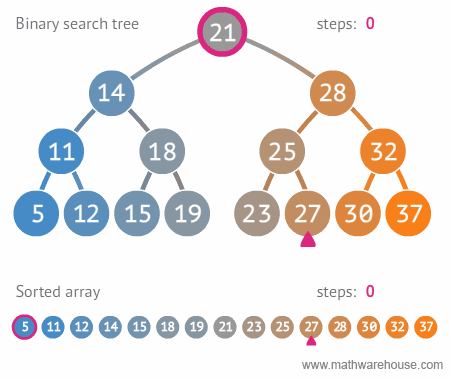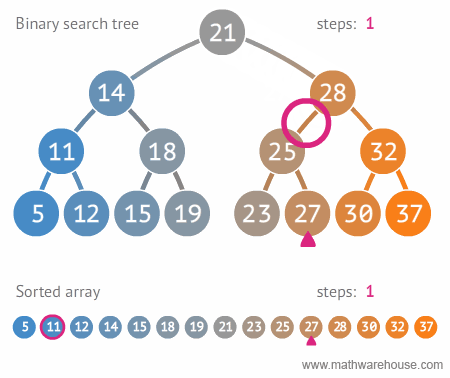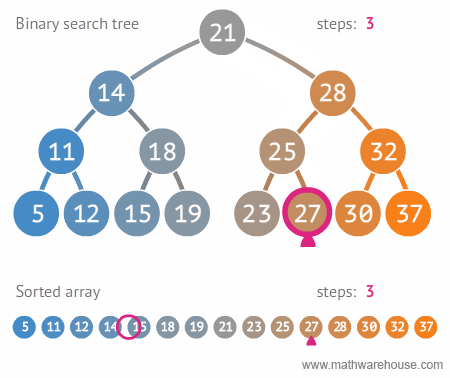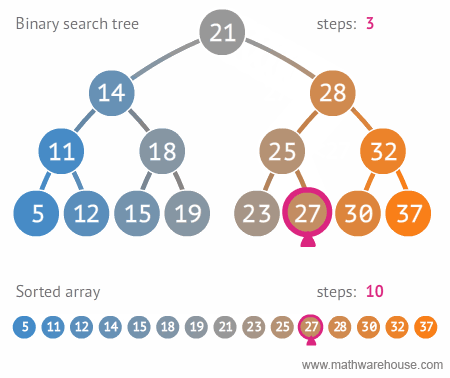
이진트리와 정렬된 배열간의 탐색 비교
📌 Python 링크드 리스트에 이진 탐색 트리 적용하기
Python 자료 구조 중 링크드 리스트가 있습니다.
링크드 리스트에도 노드 개념이 있는데요.
기존 배열에 새로운 노드를 추가하는 개념이 Tree와 유사하기 때문에,
이진 탐색 트리를 적용하여 노드 기준으로 링크드 리스트를 생성할 수 있습니다.
노드 클래스 생성
이진 탐색 트리를 고려하여, node안에 left, right property를 추가합니다.
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None이진 탐색트리에 데이터 삽입
value값으로 데이터가 들어오면, 기존 노드 기준으로 값을 비교합니다.
기존 노드 보다 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 하여
그 곳에 노드가 없으면 새로 생성하고, 있다면 다시 비교를 시작하며 트리 구조를 형성합니다.
class NodeMgmt:
def __init__(self, head):
# 처음 들어가는 node는 root node
self.head = head
def insert(self, value):
self.current_node = self.head
while True:
if value < self.current_node.value:
# node기준 왼쪽으로 이동.
if self.current_node.left != None:
self.current_node = self.current_node.left
else:
# 새로운 노드 생성
self.current_node.left = Node(value)
break
else:
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break- head node를 가진 구조의 객체 생성
head = Node(1)
BST = NodeMgmt(head)
BST.insert(2)이진 탐색 트리 자료구조를 탐색하는 메서드 search
해당 NodeMgmt 클래스에, 입력된 value 값을 기준으로 트리 구조를 탐색하는 search 메서드를 추가합니다.
# value값과 같은 값을 찾기 위한 메서드
def search(self, value):
self.current_node = self.head
while self.current_node:
if self.current_node.value == value:
return True
elif value < self.current_node.value:
self.current_node = self.current_node.left
else:
self.current_node = self.current_node.right
return False - BST라는 객체를 생성하고, 값을 넣은 후 search method Test
head = Node(1)
BST = NodeMgmt(head)
BST.insert(2)
BST.insert(3)
BST.insert(0)
BST.insert(4)
BST.insert(8)
BST.search(8)
# True반응형
'APS' 카테고리의 다른 글
| [Python] Hash Table의 충돌 개선을 위한 SHA-1, SHA-256 (0) | 2022.10.04 |
|---|---|
| [Python] Hash Table에 Linear Probing 기법 적용하기 (0) | 2022.09.27 |
| 이진트리(Binary Tree) - 전위순회, 중위순회, 후위순회 (0) | 2021.04.15 |
| 파이썬 APS_탐색 알고리즘 DFS / BFS (0) | 2021.03.03 |
| 정렬(Sort) 알고리즘_버블 정렬, 카운팅 정렬 (0) | 2021.02.18 |
